ALCCS

Code: CS21                                    Subject: DATA STRUCTURES & ALGORITHM DESIGN

Time: 3 Hours                                                                                                     Max. Marks: 100

NOTE:  

· Question 1 is compulsory and carries 28 marks. Answer any FOUR questions from the rest.  Marks are indicated against each question.

· Parts of a question should be answered at the same place.

Q.1      a. Compute the average case complexity of linear search algorithm.

b. Derive the equation for computing the address of the memory location of an element stored in n-dimensional array.

             c.  Write the advantages of doubly linked list over singly linked list.

             d.  Convert the following infix expression into postfix expression

                               A*B+C/D-A*F

             e.  Write binary search algorithm.

             f.   In array implementation of Queue without shifting the element of queue after deletion of an element from the queue. Explain the mechanism used to clearly distinguish between queue full and queue empty?

             g. Define minimum spanning tree and also explain it with the help of an example.          (7  4)

Q.2       a. In algorithmic complexity show that the lower order terms and constant do not matter and are ignored.        

             b.  Work out the time complexity of merge sort in the worst case.

             c.  Write algorithm for Push and Pop operations of a stack implemented using linked list.

(6+6+6)

Q.3     a.  A Binary search tree contains integers in each node. Write a function which examines a BST and returns 1 if a target value is found on the BST, else it returns 0.                                                              

b. Explain the basic principle of dynamic programming using a simple example.                (10+8)

  Q.4     a.   Write algorithm for addition of two polynomial represented by linked list.

b.  Show the outcome of different passes for sorting the following sequence of data using quick sort algorithm. 

                                        8, 11, 3, 15, 6, 9, 12, 39

                  Choose the first element as pivot.

             c.  Construct AVL tree for the days of week on their lexicographical order. Initial order of the days is as they occur in a week from Sunday to Saturday.                                                                      (6+6+6)

Q.5     a.  In a circular queue show the conditions that differentiate between empty queue and full queue. Also explain disadvantages of implementing queue (non circular) using array.                                         

             b.  Construct a binary tree for the following postorder and inorder traversal sequences.           

                  Postorder: GHDIEBFCA

                  Inorder:    GDHBEIACF

             c.  Construct a B tree of order 5 for the following sequence of data. Also show the tree after deletion of 106 from the tree constructed.

                           87, 140, 23, 62, 74, 90, 100, 106, 152, 186, 194, 102                               (6+6+6)

Q.6     a.  What is adjacency list representation of a graph? Explain with the help of an example. Also write its advantages over adjacency matrix representations of graph.                                                                

             b.  Given the following graph apply Depth First search and list the vertices in the order they would be visited. If nodes at same level, then do alphabetical ordering. Start with node K.

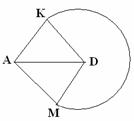
c.  Write Dijkstra’s algorithm to find shortest path in a Graph.                                    (6+6+6)

Q.7       a.  What is threaded binary tree? Write its advantages over binary tree.                                  

             b.  Write a recursive algorithm that determine the height of a binary tree.                                 

c.  Write a function which deletes the last element of a singly linked list.                       (6+6+6)