ALCCS

Code: CS21 Subject: DATA STRUCTURES & ALGORITHM DESIGN

Time: 3 Hours Max. Marks: 100

NOTE:

· Question 1 is compulsory and carries 28 marks. Answer any FOUR questions from the rest. Marks are indicated against each question.

· Parts of a question should be answered at the same place.

Q.1 a. An algorithm runs a given input of size n. When n is 4096 the run time is 512 milliseconds. Also when n is 16384, the run time is 2048 milliseconds. What is the complexity? What is the big-O-notation?

b. Imagine we have two empty stacks of integers, s1 and s2. Draw a picture of each stack after the following operations.

pushStack(s1,3);

pushStack(s1,5);

pushStack(s1,7);

pushStack(s1,9);

while (! emptyStack(s1))

{

popStack(s1,x);

popStack(s1,x);

pushStack(s2,x);

}

c. How does doubly linked list differ from circular linked list? Explain.

d. Convert the following infix expression into prefix expression

(A+B)*C/(A+D)

e.

Draw the threaded tree corresponding to the following binary tree showing the threads (Fig.1).

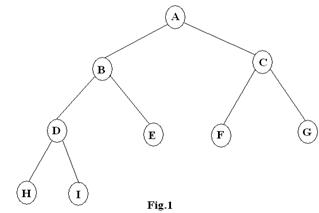
f. Given the following array:

80 72 66 44 21 33

After two passes of a sorting algorithm the array has been rearranged as shown below:

21 33 80 72 66 44

Which sorting algorithm is being used (selection, bubble, insertion). Defend your answer.

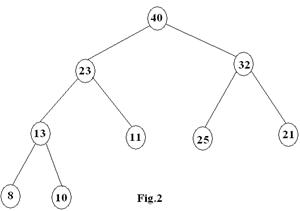
g. Insert 38 in the heap in the following figure. Also explain the method of getting the new heap after insertion (Fig.2). (7 4)

Q.2 a. Discuss the worst case performance of selection sort.

b. Reorder the following complexity from smallest to largest:

2ⁿ, n!, n¹⁰,2⁴, nlog₂(n).

Justify your answer.

c. Calculate the big-O notation of and 3n⁴+nlog₂ (n) (9+5+4)

Q.3 a. Show that the maximum number of nodes in a binary tree of depth k is 2^k-1, k1.

b. Construct the binary tree whose preorder and inorder sequences will be

A B C D E F G H I

B C A E D G H F I

respectively. Explain the steps.

c. Define the terms:

(i) An m-way tree

(ii) B-tree (6+6+6)

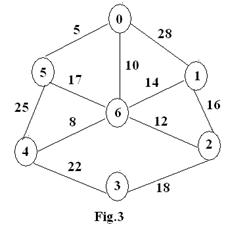
Q.4 a. Explain the Kruskal algorithm. Using the algorithm find a minimum spanning tree of

the weighted graph shown in Fig.3. Will it be the unique minimum spanning tree?

State reasons for your claim.

b. What do you understand by garbage collection? Discuss the best fit and worst fit memory allocation methods. (11+7)

Q.5 a. Explain quick sort algorithm.

b. Using Dijkstra’s algorithm, find the shortest path between node A and all the remaining nodes in the following graph (Fig.4). (9+9)

Q.6 a. How many keys can a B-tree of order m and height h hold? Justify your answer.

b. Write an algorithm to determine a given string is a palindrome. Note that a string is a palindrome if it can be read forward and backward with the same meaning. Capitalization and spacing are ignored. For example, anna and go dog are palindromes.

c. The following binary search tree is given in Fig.5.

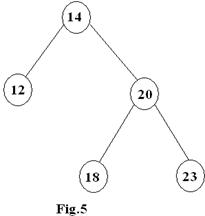
(i) Is it an AVL tree? State reasons for your claim.

(ii) Add the key 44 in the above tree so that it becomes an AVL tree. (4+6+8)

Q.7 a. Write a short note on any THREE of the following:

(i) Huffman codes

(ii) Merge sort

(iii) Boundary tag method

(iv) Representation of sparse matrix using list structure (6+6+6)