ALCCS
Code: CS40 Subject: COMPUTER GRAPHICS
 Time: 3 Hours
Max. Marks: 100
Time: 3 Hours
Max. Marks: 100
NOTE:
· Question 1 is compulsory and
carries 28 marks. Answer any FOUR questions from the rest. Marks are indicated against each question.
· Parts of a question should be
answered at the same place.
· All
calculations should be up to three places of decimals.
Q.1 a. What do you understand by
vanishing points? Indicate how do you
calculate the vanishing point when viewing a 3D object.
b. Indicate
very briefly the scan line seed fill algorithm.
c. Consider
a clipping window A (10, 10), B (40, 10), C (40, 20), D (10, 20). Using
outcodes of end points of the line P (50, 0) – Q (70, 30), show that the line
is trivially invisible.
d. Consider
a triangle A (a,b), B(c,d), C(e,f) drawn on the XY plane. Find the
transformation matrix to perform 90o
clockwise rotation transformation about the point A? Also find the coordinates
of the rotation of B and C?
e. Given
the control points P1( 0,10), P2( 30,40), P3(80,10), P4(60,40), draw a rough
sketch of a cubic Bezier curve, and draw the convex hull of the curve. You
don’t have to do any calculations.
f. Explain
briefly the floating Horizon method for hidden surface removal.
g. A
light source of intensity I is throwing light on an object at distance D. Write
an expression for the diffuse reflection from the object. Define any constants
that appear in your expression. (7 ![]() 4)
4)
Q.2 a. It
is desired to draw a line in the first quadrant, with slope m = 2. Derive the
Bresenham’s integer line drawing algorithm to indicate the coordinates of the
line that will be displayed, as the line moves from P(x1 , y1)
to Q(x2 , y2), given that
x2
> x1 and y2
> y1.
b. Compare
Gouraud shading with Phong shading in terms of their implementation and the
difference in appearances in displaying an object on the screen. (10+8)
Q.3 a. Consider a clipping window A (0,
0), B (30, 0), C (30, 20), D (0, 20). Use Cyrus Beck algorithm to determine the
portion of line P (25, 40) – Q (50, 10) clipped by this window. Make the
complete Cyrus Beck table and show all calculations.
b. Explain
the Binary space partitioning method for hidden surface removal. (10+8)
Q.4 a. Derive the parametric form of the cubic Bezier
curve. Show that the last point on the curve coincides with the last control
point, and that the starting slope of the curve is fixed by the position of the
first two control points.
b. Consider the rectangular object
shown in Fig. 1. Note that the Z-axis is coming towards the observer from the
origin of the axes. Work out the transformation matrix to rotate the object
clockwise around Y-axis by 30o and to translate it by 10 units along
the Z-axis, such that the new coordinate of point O is (0, 0, – 10). (10+8)
Q.5 a. Derive the transformation matrix
to obtain an isometric view of the object shown in Fig. 1.
b. Describe
antialiasing in computer graphics. (10+8)
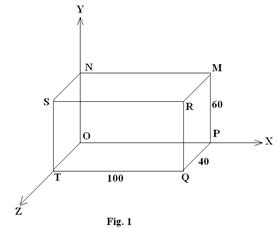
Q.6 a. The object shown in Fig 1 is
pushed back 40 units along z axis till the face SRQT falls on the XY plane. It
is then pushed to left along x axis by 50 units such that new coordinate of T
is (–50,
0, 0). Work out the transformation matrix for the perspective view that will be
generated from a centre of projection at (0, 0, 25). Calculate the screen
positions of points S, R, N and M as viewed from this position.
b. Taking the Koch curve as an
example show how the fractal dimensions are calculated for self similar
fractals. (12+6)
Q.7 a. Describe the transformation
matrix to obtain the top view and the right side view of the object shown in
Fig 1.
b. Given 4 control points P1 (40,
40), P2 (10, 40), P3 (60, 60), P4 (60, 0), draw a rough sketch
of a periodic cubic B-spline curve.
Calculate the position of the last point on the
curve. Given another control point P5(80,20), show that the starting point of
the B- spline curve corresponding to control
points P2, P3, P4, P5 is same as the last point of the
first curve. The characteristic basis matrix for a periodic cubic B-spline
curve is given by (6+12)

(1/6) – 1
3 – 3 1
3 –
6
3 0
– 3 0 3 0
1 4 1 0