ALCCS   -   NEW SCHEME

 

Code: CT11                                                         Subject: DATA STRUCTURES THROUGH C

Flowchart: Alternate Process: SEPTEMBER 2010Time: 3 Hours                                                                                                     Max. Marks: 100

 

NOTE: 

·      Question 1 is compulsory and carries 28 marks. Answer any FOUR questions from the rest.  Marks are indicated against each question.

·      Parts of a question should be answered at the same place.

 

 


Q.1                                                                                                                                           (74)

          a. State two important differences between a pointer and an array.

          b. Assume A = 1, B = 2, C = 3. Evaluate the following postfix expression:

                                    ABC + * C B A - + *

                c. Write a function, length, in C that will return the number of nodes in a given singly linked list.

             

          d. Represent the polynomial 3x14 + 2x8 - 1 using linked list.

 

       e. Do the preorder and inorder sequences of a binary tree uniquely define the binary tree? Justify your answer.

          f. Let the adjacency matrix of a graph G be given as

 


                                                0     1          1          1

                                         

                                           1     0          1          1

 

                                           1      1         0          1

 

                                           1      1         1          0

                            

                  find the graph G?
 
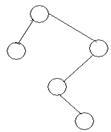
          g. Determine whether the following binary search tree is an AVL tree? Give reasons for                                       your claim.       

                                                                                                                                               

     

 

 

 

Q.2   a.   Write a C program to add a new given node at the end of a singly linked list.

          b. Let G be an undirected connected graph given by 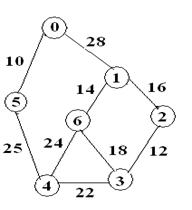                                                                                                                                                                                       Using Kruskal’s algorithm generate a minimum cost spanning tree.                (9+9)                                                                                                                                                                                                                        

 Q.3   a. Write an algorithm to determine the number of nodes in a given binary tree? 

     

          b. For the following input list of numbers

                     14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

               Find the binary search tree?                                                                           (9+9)

     

 Q.4    a. Write a function in C program that traverses a threaded binary tree in preorder.

 

          b. Show that the maximum number of nodes in a binary tree of depth K is

                         2k – 1, k ≥ 0                                                                                                      (9+9)

 

     

  Q.5  a. With an example, explain the working of heap sort algorithm.

     

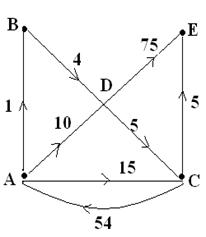
          b. Find the shortest path using Dijkstra’s algorithm in the given weighted directed graph from A to E. Explain the steps.                                                                                                                                                                                                            (9+9)

                                                          

 

                           

 

 

 

Q.6    a. Discuss boundary tag method and write a C program for freeing memory blocks.  

         

          b.  If a binary search tree with n nodes is well balanced, what is the approximate number of

               comparisons of keys needed to find a target? What is the number if the tree degenerates

               to a chain?                                                                                                            (9+9)

 

 Q.7      Write short note on any THREE of the following:-

 

                        (i)   Circular queue and priority queue

                        (ii)  Huffman trees

                        (iii) Shell sort

                        (iv) Game trees                                                                                                            

 

             .                                                                                                                            (36)