ALCCS

 

Code: CT22                                       Subject: DISCRETE MATHEMATICAL STRUCTURES

Flowchart: Alternate Process: SEPTEMBER 2010Time: 3 Hours                                                                                                     Max. Marks: 100

 

NOTE:  

·      Question 1 is compulsory and carries 28 marks. Answer any FOUR questions from the rest.  Marks are indicated against each question.

·      Parts of a question should be answered at the same place.

 

 

 

Q.1      a.  Prove that in a connected graph of “n” vertices, the number of vertices of odd degree will always be even.

 

             b.  In how many different ways can 6 people be seated in a committee room with 7 chairs?

                             

             c.  Is the statement ‘If p then q’ with given p and q, false or true?

                  p: Ravana was the king of Ayodhya

                  q: Mandodari was Ravana’s wife

 

             d.  Simplify the logical expression

 

             e.  State and prove the Euler formula to detect the planarity of a graph.

 

             f.   What is the difference between a Relation and a Function? What is an Equivalence Relation?

 

             g. What kind of strings is accepted by the following automaton? Explain how.             (7  4)

1
 
 

 

 

 

0
 
 

 

 


Q.2       a.  If P, Q and R are three atomic variables, obtain the principal disjunctive normal form for (P→ (QΛR)) V (~P→ (QVR))                                                                                                                 

            

             b.  How many bytes are required to encode n bits of data when n equals 5, 500 and 3000 respectively?                                                                                                                                (9+9)

 

  Q.3     a.  Show that the maximum number of vertices in a binary tree of height h is 2h+1 – 1.

                 

             b.  On a set S = {1,2,3,4,5}, find the equivalence relation on S, which generate the partition { {1,2}, {3}, {4,5} }. Draw the graph of the relation.                                                                                  (9+9)

 

       


 
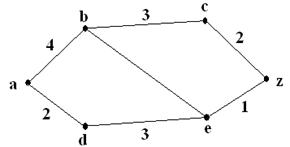
Q.4       a.  Using Dijkstra’s algorithm find a shortest path between ‘a’ and ‘z’ in the weighted graph shown below

 

 

 

 

 

 

 

 

                       

b.      Translate the infix expression

To reverse polish expression.                                                                              (9+9)

       

  Q.5     a.  Show that the language

                 

                  is not a finite state language.

 

             b.  Define Boolean algebra. Prove that the power set of any set will form a Boolean algebra. (9+9)       

  Q.6     a.  What is a lattice? Which of the following graphs are lattices? State reasons for your claim.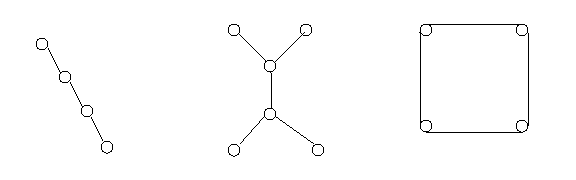

                                            (a)                                       (b)                                             (c)         

 

             b.  Prove that if (A, ≤) has a least element, then (A, ≤) has a unique least element.         (8+10)

 

  Q.7     a.  Write the Preorder, Inorder and Postorder tree traversal algorithm.

 

             b.  For the given graph, find the minimal spanning tree using Prim’s algorithm.                (10+8)